什么是哈希函数

今天我们来看看比特币的一个重要概念：哈希函数。本文首先介绍了什么是哈希函数以及哈希函数的抗碰撞性、隐秘性和谜题友好三大特性。再结合区块链的特性，分享了哈希函数在区块链挖矿工作量证明中的具体应用，并简单讲解了哈希函数与防篡改性的关系。

全文约2600字，大概需要阅读8分钟。

01

     什么是哈希函数

 

哈希函数（Hash Function）是加密算法哈希算法中广泛应用的一种函数，也称为散列函数或杂凑函数。哈希函数作为公开函数，可以将任意长度的消息M映射成为一个长度较短且长度固定的值H（M），称H（M）为哈希值或者消息摘要（Message Digest）。哈希运算是一种单向密码体制，即一个从明文到密文的不可逆映射，只有加密过程，没有解密过程。它的函数表达式为：

y = H（x）

安全哈希算法（Secure Hash Algorithm 256，SHA-256）是比特币经常使用的一种哈希函数，本文主要以 SHA-256算法为例。无论输入是什么数字格式、文件有多大，哈希运算输出的都是固定长度的比特串，比如在二进制下有256bit，即256 个0或者1组成的串，用16进制数字表示的话是64位，例如：

我们常用的16进制：

0xd7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592

转为2进制：

1101011110101000111110111011001100000111110101111000000010010100011010011100101010011010101111001011000000001000001011100100111110001101010101100101000111100100011011010011110011011011011101100010110100000010110100001011111100110111110010011110010110010010

 

02

哈希函数的三大特性

 

要使哈希函数达到密码安全，需要附加以下三个特性：碰撞阻力、隐秘性、谜题友好。

特性1：碰撞阻力

Hash 函数 H 将可变长度的数据块 M 作为输入，产生固定长度的 Hash 值 h =  H(M)。称 M 是 H 的原像。因为 H 是多对一的映射，所以对于任意给定的 Hash 值 H，对应有多个原像。如果满足 x ≠ y 且 H(x) = H(y)，即两个不同的输入 x 和 y 产生相同的输出 H(x) = H(y)，则称为碰撞。如果对于哈希函数 H(x)，没有人能够找到碰撞，则称该函数具有碰撞阻力。

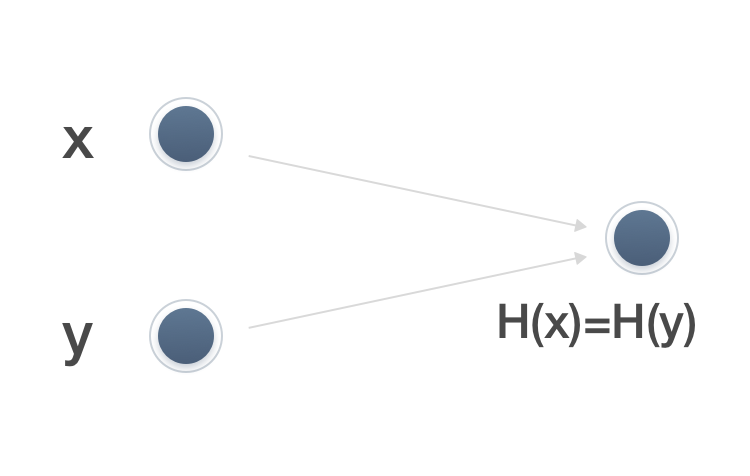
对于给定的数据 X ,很容易算出哈希值 H = H(M)；但根据 H 很难反算出 X；很难找到 X 和 Y 使得 H(X) = H(Y)。事实上，把大空间的消息压缩到小空间上，碰撞肯定是存在的。

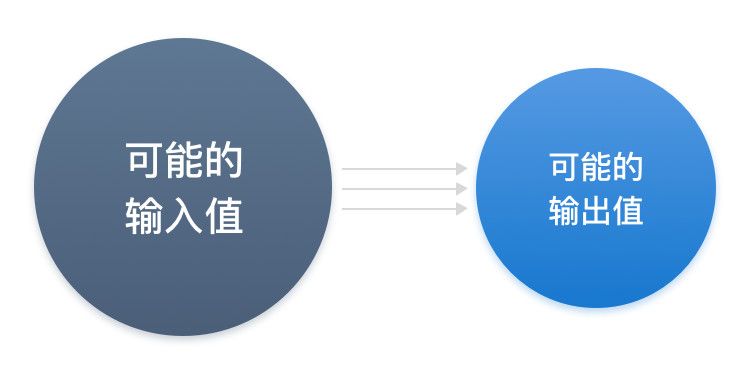
假设哈希值长度固定为256位，如果顺序取1，2，…2^256+1，这2^256+1个输入值，逐一计算其哈希值，肯定能找到两个输入值使得其哈希值相同。但不要高兴的太早，因为你得有时间把它算出来，才是你的。

对于哈希值长度为256位的哈希函数，平均需要完成2^128次哈希计算，才能找到碰撞对。如果计算机每秒进行10000次哈希计算，需要约10^27年才能完成2^128次哈希计算。

 

特性2：隐秘性

隐秘性指的是当输入 r 选自一个高阶最小墒的概率分布，在给定 H(r||x) 条件下确定 x 是不可能的。简单的说，就是无法从输出得到输入。设 y=H(x) ，如果我们知道 y，很难迅速找到满足符合条件的 x，则称哈希函数 H(x) 具有隐蔽性。隐蔽性意味着几乎不可能找到其反函数 x’=H'(y)，实际上满足条件的 x 应该多个，这里隐蔽性要求哪怕1个也找不出来。这是因为上面提到的哈希函数单向性，对于给定的Hash值，在 2^128次哈希计算量下是不可行的。

隐秘性的一个应用是“承诺”，将信息（message）和一个随机数(nounce)作为输入，所得的输出即为承诺。这里的承诺包含两方面的意思：通过承诺，其他人无法知道你的输入；而你一旦公开了承诺，你无法欺骗别人该承诺是另外一个信息。所以，这里应用到了隐秘性。此外，每次的承诺都需要一个新的的随机数，这对承诺的安全性很重要。

 

特性3：谜题友好

如果对于任意 n 位输出值 y，假定 k 选自高阶最小熵分布，如果无法找到一个可行的方法，在比2的 n 次方小很多的时间内找到 x，保证 H(k||x) = y 成立，那么我们称哈希函数 H 为谜题友好。在搜索谜题这个应用中，我们将建立一个搜索谜题，该谜题是一个需要对庞大空间进行搜索，才能找到解决办法的数学问题。简单来说，就是要求具有随机性，任意输入可以得到固定位数的输出，很难找到输入和输出之间的任何关联性，哪怕是稍微调整输入，得到的输出都具有随机性，除了通过调整输入内容进行“暴力试算”，没有其他更好的办法。

碰撞阻力，隐秘性，谜题友好，各有侧重，而又相互贯通。特别是隐秘性和谜题友好，十分相似，对于想深度理解的读者，需要指明的是隐秘性说的是确定x，谜题友好说的是找到k。对于哈希函数 H(x)，我们做出如下总结：

• 对于 y = H(x)，知道 x 计算其哈希值 y 很简单；
• 碰撞阻力：很难找出不同的x,y，使得 H(x) = H(y)；
• 隐秘性/谜题友好（近似理解）：对于 y = H(x)，知道哈希值 y ，很难反求出x。

 

03

哈希函数的意义所在

 

哈希函数与工作量证明

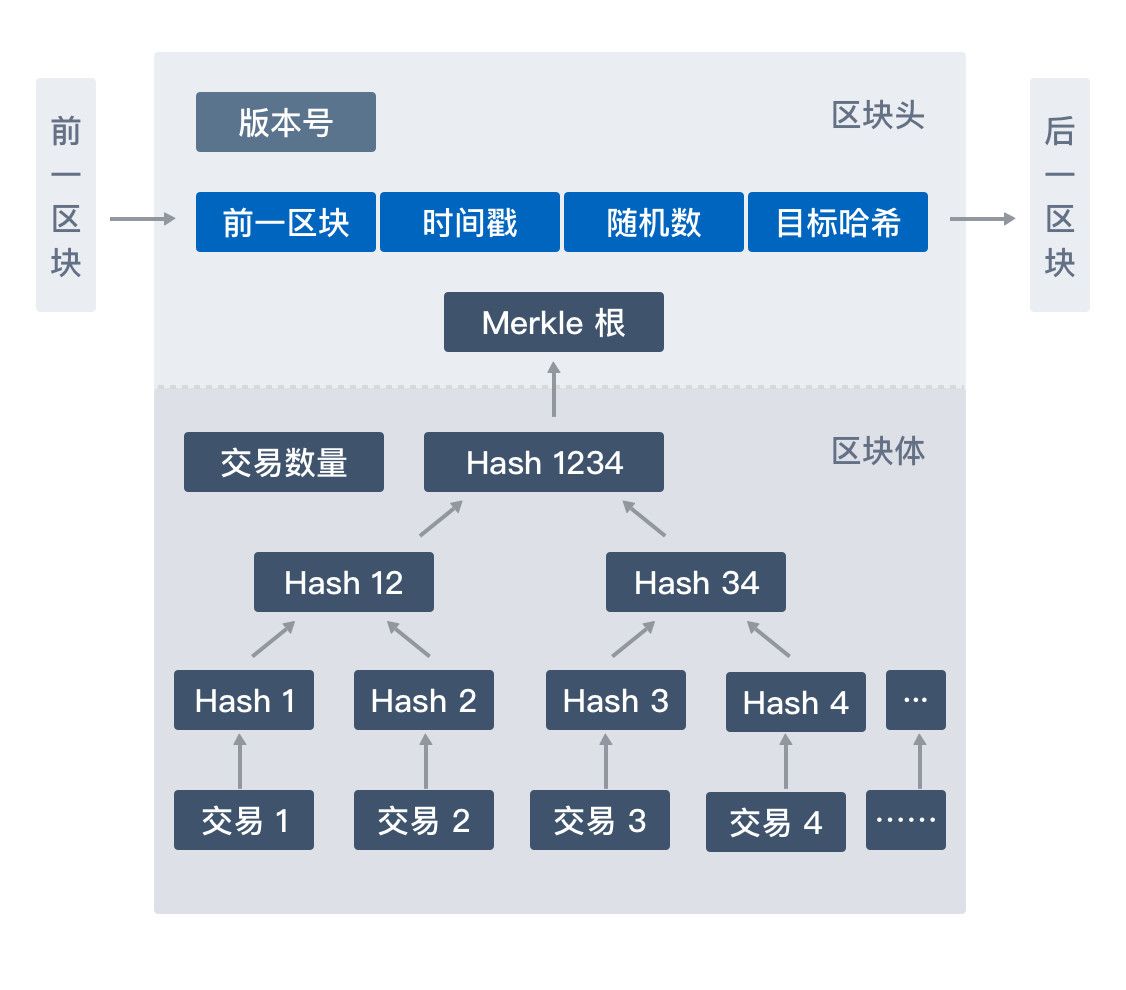
先回忆一下区块结构。比特币的区块由区块头及该区块所包含的交易列表组成，区块头的大小为80字节，由4字节的版本号、32字节的上一个区块的散列值、32字节的 Merkle Root Hash、4字节的时间缀（当前时间）、4字节的当前难度值、4字节的随机数组成。区块包含的交易列表则附加在区块头后面，其中的第一笔交易是 coinbase 交易，这是一笔为了让矿工获得奖励及手续费的特殊交易。

区块的大致结构如图所示：

 

 

其中：

• Version 是当前区块的版本号
• 该区块所包含的多个交易的 Hash 值构成区块的 Merkel 数据结构
• nbits 是当前比特币协议设定的计算复杂度
• ntime 是区块的时间戳
• pre_hash 是前一个区块的 Hash 值

Hash(L,x) = SHA256(SHA256(block_header))

block_header = version + Merkel + nbits + ntime + pre_hash

拥有80字节固定长度的区块头，就是用于比特币工作量证明的输入字符串。不停的变更区块头中的随机数即 nonce 的数值，并对每次变更后的的区块头做双重 SHA256运算（即 SHA256(SHA256(Block_Header))），将结果值与当前网络的目标值做对比，如果小于目标值，则解题成功，工作量证明完成。

小结：可以简单理解成，比特币工作量证明的过程，就是通过不停地变换区块头（即尝试不同的随机值）作为输入进行 SHA256哈希运算，找出一个特定格式哈希值的过程，即要求有一定数量的前导0，而要求的前导0的个数越多，代表难度越大。

 

哈希函数与防篡改性

当 x 只变化一个字节，y 是不是也会只变化一个字节，这种微小的差异是否能篡改事实？

不能！

如果输入 x 有1bit 的变化，散列结果即哈希值中将有一半以上的 bit 改变，这又叫做“雪崩效应（avalanche effect）”。

区块链之所以称为链，是因为每一个区块都保存了前一区块的目标 Hash值（创世块没有前一 Hash 值）。某一个区块的某一笔交易发生篡改，因为默克尔树算法的作用这个区块的目标 Hash 值就会被改变，并导致连锁反应。以这个区块为基础，后续所有区块的 Hash 值都会发生变化，任一记账节点都可以轻易的发现账本被篡改，这样就保证了区块链上的所有区块都具备了防篡改功能。

哈希函数的抗碰撞性用来做区块和交易的完整性验证，一有篡改就能被识别出来。

 

最后我们对本文进行归纳总结：

 

1、哈希函数输入任意长度的信息 x ，输出的哈希值 H(x)的 长度都是固定的 256bit；

2、哈希函数具有碰撞阻力、隐秘性、谜题友好三重重要特性，具体来说：

• 对于 y=H(x)，知道 x 计算其哈希值 y 很简单；
• 碰撞阻力：很难找出不同的 x,y，使得 H(x) = H(y)；
• 隐秘性/谜题友好（近似理解）：对于 y = H(x),知道哈希值 y，很难反求出 x；

3、对每次变更后的的区块头做双重 SHA256 运算（即SHA256(SHA256(Block_Header))），结果值小于目标值（有足够多的前导0），工作量证明完成；

4、哈希函数下的防篡改性意味着，输入 x 哪怕 1bit 的变化都将改变一切，所以不可篡改。