5分钟内了解默克尔树

简单来说，哈希树（默克尔树Merkle Trees）中，每个节点都标有一个数据块的加密哈希值。哈希树可以用来验证任何一种在计算机中和计算机之间存储、处理和传输的数据。它们可以帮助确保在点对点网络中从其他对等体收到的数据块是原封不动地收到的，且没有损坏，也没有改变。

那么让我们来讨论一下默克尔树吧。

说到区块链，我们有很多区块，这些区块会通过哈希值的帮助连接在一起，我们知道每一个区块都会拥有交易，可以是一个，也可以是100多个，那么如果我们想要找出区块本身的哈希值，我们该怎么做呢？是把整个区块组合起来形成一个哈希值呢？还是要找到每个交易的哈希值？现在如果你想找到每个交易的哈希值，你必须存储所有的哈希值，这样一个区块就不会只有1个哈希值，而是有100个哈希值，我们不希望我们只想得到1个哈希值，而其中一个实现的方法就是借助默克尔树。

第一次看到默克尔树时，它们可能会非常混乱，但实际上结构非常简单。

每一棵树都会有一个根，一组枝条，然后叶子从枝条的底部长出。

那么要如何建立这棵树呢，让我们想象一下，在一个区块中，我们有8个交易，而我们将开始收集每个交易的哈希值，那么对于8个交易，我们将会有8个哈希值。现在，我们要做的是就找到第一个和第二个的值，然后是第三个和第四个，以此类推，直到最终得到这样的东西：

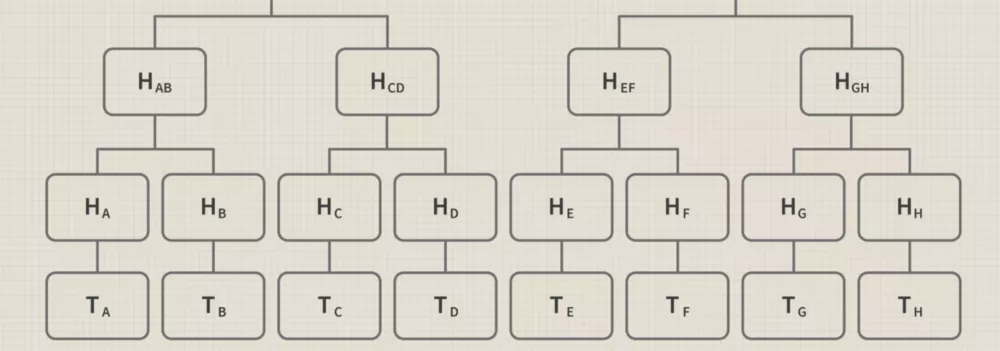
一旦我们有了所有的集体哈希，我们就可以再次将它们组合起来，如下图：

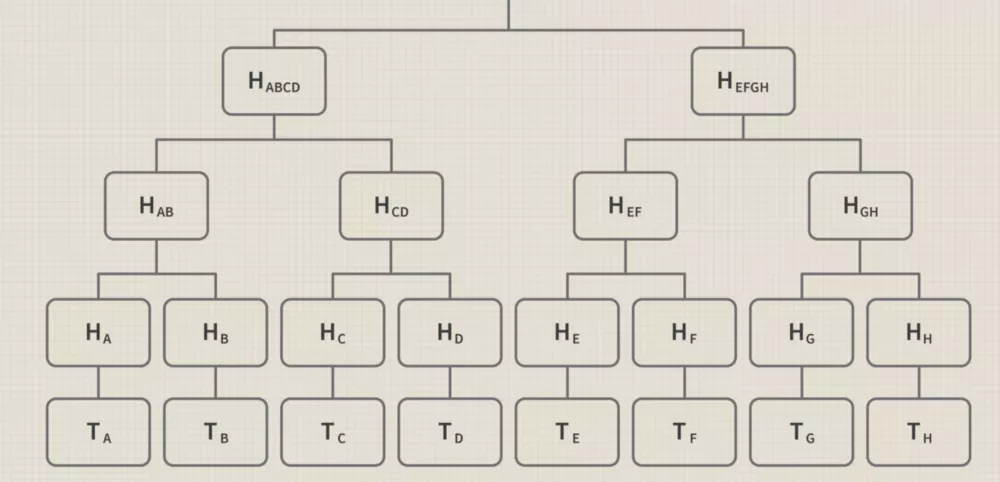
最后在完成上述步骤后，我们将回到树的根部，最终的默克尔树则会入下图所示：

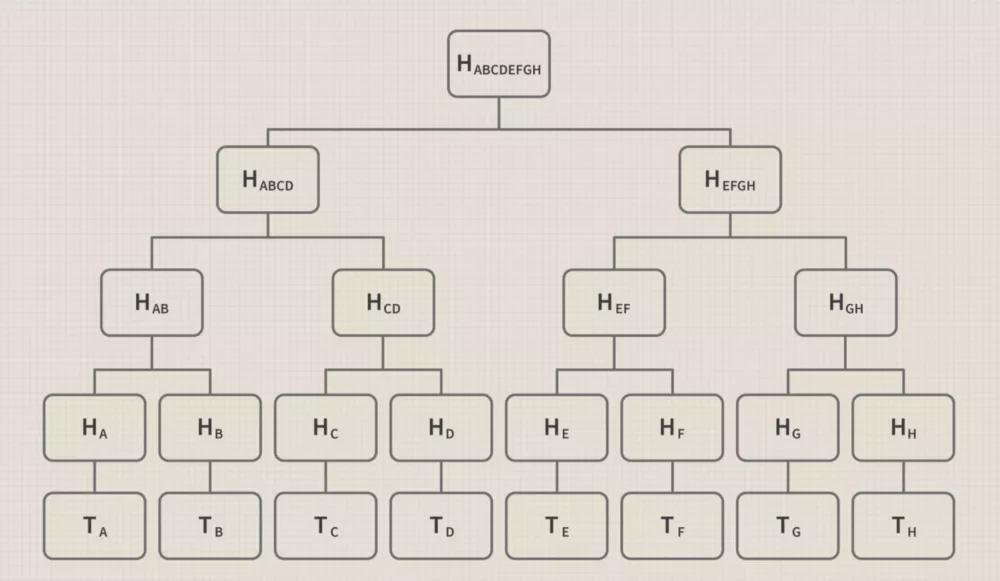
然后在最后我们会把所有的东西结合起来，得到1到8的哈希值，然后给整个区块和里面所有的交易标记上一个整体的哈希值。

在这个例子中，我们可以看到最后是偶数，但是如果是一个奇数会是怎么样呢？我们只需重复交易，如[9，10，9，10]分支中所示的那样。

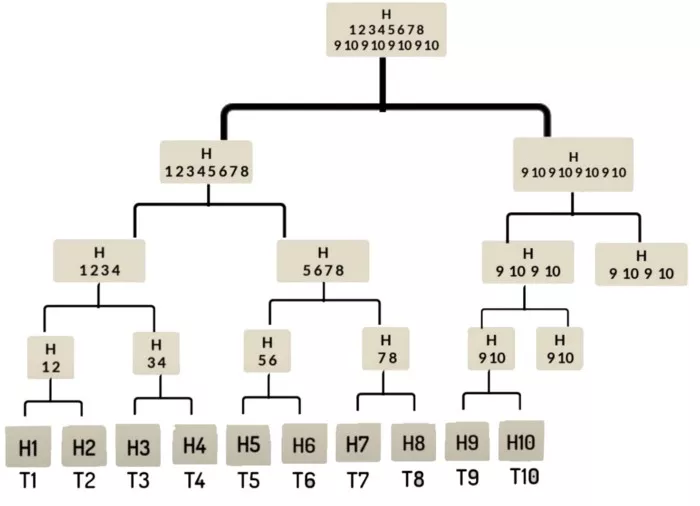
最后，当我们在根部将所有这些组合在一起时，我们将留下默克尔树的根部，且只有1个区块的哈希值。这在涉及区块链时，是非常有用的，因为它限制了能够处理所有区块所需的内存，能够只处理每个区块的一个哈希值，因此比必须处理每个区块内存储的100个哈希值要高效得多。

大多数哈希树的实现都是二进制的，这意味着每个分支下都会有1个叶子，但它们也一样可以在其分支下使用更多的叶子节点。